• —
  —
  — Places
  • 
    Topical index and search

    Best way to find most things

  • Biology Worthy of Life: main page

    Bringing biology back to life

  • Book: Organisms and Their Evolution

    Let’s take living beings seriously

  • List of all major articles since 2009

    With descriptions of the articles’ content.

  • Latest news

    News of interest to readers of this site

  • Primary Nature Institute website

Organisms and Their Evolution
A book by Stephen L. Talbott

Puzzles of the Microworld

All physical scientists, in an effort to understand reality, take their stand upon a tiny island of knowledge, surrounded by an immense, fathomless sea of ignorance. The island is forever threatened and re-shaped by revelatory eruptions from the surrounding deep.

According to the celebrated physicist, Richard Feynman, "we have no knowledge of what energy is" (Feynman et al. 1963). Nor, for that matter, do we know what a force is. And the same is true of all the foundational terms of physics. Matter, the supposedly solid ground of material reality, remains an enigma that has only grown more perplexing along with advances in quantum physics. Other basic terms such as “space”, “time”, and “field” — while perfectly workable as conceptual black boxes in the context of the physicist’s narrow mathematical aspirations — are not themselves so much elements of adequate explanation as they are perplexities in need of explanation.

The general fact of chemical transformation, by which, for example, hydrogen and oxygen gases can be made (in the right proportions and in the presence of a flame) to “explode” into water, remains for our present understanding something like a miracle. The supposedly explanatory “particles” involved — which we know only as abstract, mathematized constructs altogether lacking sensible qualities — are said to rearrange themselves in an instant. According to the standard picture, the rearrangement of the qualityless particles somehow yields a radical transformation in the qualities of the reacting gases, releasing in the process a great amount of Feynman’s unknown energy. And so, gaseous elements of the atmosphere, flown through by birds, transmute before our uncomprehending eyes into a fluid element of the sea, swum through by fishes.

The mysteries we confront are as great as the universe itself. Physical laws — and, in general, the rational coherence and order of the world — remain puzzles for us at least as profound as they were for Galileo and Newton. And so also with the ever-growing conundrum of human thought — that “unnatural quirk” in the universe in terms of which, it just so happens, the universe bares for us something of its most intimate nature. As for the “Big Bang”, it brings no more lucidity to the question of origins than “God made it so”.

It would be a stretch to think that any of our “settled” science is immune to serious reconsideration, depending on whatever revelations eventually illuminate these fundamental questions. I am not talking about a need to recalculate, say, the numerical value of the gravitational constant, but rather our understanding of the character of the physical cosmos and the manner of our participation in it as knowers. Or the significance, among scientists, of their paradoxical commitment to a materialist dogma at a time when no one can define “material” but all do consider themselves thinkers who take their own scientific descriptions to be both meaningful and true to the world’s reality.

In sum: our accumulating grasp of (mostly technological) know-how, stunning as it is in practical terms, is nevertheless a power enveloped by profound ignorance. What little understanding we have of the world we so skillfully manipulate is at every moment subject to modification by whatever yet-unimagined insights may eventually bring clarity to this or that enigmatic term at the root of our science.

And yet — isn’t it odd? — we find it so natural and easy to forget all this! In our primary cognitive enterprises — science, education, religion — training for the young focuses on what we already know, or think we know, rather than on our ignorance and the corresponding promise of new understanding. On my own part, I feel an obligation at least to acknowledge the largely unaddressed mysteries shadowing our understanding.

So when we talk about the diverse environments in which organisms live, one aspect of the diversity has to do with their varying experiences of the force of gravity in relation to the dimensional aspects of their lives. To be a different size is already to live in a different world.

Einstein, so it is said, was led to his theory of special relativity due in part to his having imagined what it would be like to “ride on a light beam”. Might we possibly discover equally strange things if we tried to imagine what it would be like to dwell within an individual living cell?

Unlike Einstein with his task, ours would be much simpler. It would not require bold new understandings in physics, but simply a willingness to imagine the changing play, at different dimensions, of already formulated physical laws. And, fortunately, we have at least one scientific paper, written over thirty years ago, that has already done much of the work of imagining the startlingly different conditions of life at the scale of the cell.

That 1990 paper was written by Guenter Albrecht-Buehler of the Northwestern University Medical School in Chicago. He began his professional life as a physicist before moving into cell biology. However, unlike what you might expect of a physicist, one of his larger concerns was rooted in the conviction that we cannot build up an understanding of organisms by starting from the molecular level. His paper, titled “In Defense of ‘Nonmolecular’ Cell Biology”, has not, in my judgment, received the attention it deserves. The present chapter represents my effort to summarize only that part of the paper dealing with the wildly unexpected consequences of differences of scale, and then to offer a few additional comments of my own.

Unless otherwise indicated, quotes in the following section are drawn from Albrecht-Buehler’s paper.

Warning: This chapter is a bundle of contradictions. In fact, that is more or less its point. The ways we think and speak about the submicroscopic world are almost guaranteed to be impossibly off the mark, and yet anyone who would point this out has no choice but to use the established, off-the-mark language, which is the only language we currently have available. So if you begin to notice a jarring dissonance between the intended meaning and the actual language of particular statements — and I hope you will — you can take it as a sure sign that you are getting the point of the chapter.

For example, you will hear me saying that “If you considered two isolated electrons to be point masses and placed them 1 meter apart …” You will likewise hear me talking about the “collisions” of “particles”, and you will listen to a prominent cell biologist remarking how the 5 billion proteins in a cell are “jammed shoulder to shoulder, [while] also charging past one another at insanely high speeds”. These references to “isolated electrons”, “point masses”, “collisions”, and “proteins charging past one another” all seem to demand that we imagine particular things acting in the manner of the familiar objects of our experience.

But, as I hope you will realize by the end of the piece, there are no things “down there” of the sort we almost inevitably find ourselves imagining. What is down there is a very good question. And if you are asking it by the time you finish reading this, then the chapter will have accomplished its purpose.

Figure 15.1. A dew droplet on a leaf. The droplet is about one millimeter in diameter.³

Albrecht-Buehler compares the effects of viscous drag upon two objects moving through water — a spherical cell, and a sphere with a 50-centimeter diameter. Both spheres are assumed to consist of the same protein matrix. He asks: If an initial movement of one diameter per second is imparted to both of them, how quickly would they come to a stop due to the resistance of the water? It turns out that the larger sphere will travel long enough to traverse many diameters. By contrast, the cell-sized sphere will stop within about a millionth of a second, during which it will have traveled about a millionth of a diameter — which is more or less to say that it stops immediately and doesn’t travel at all.

This might seem to suggest that if you or I lived at the size of a cell — or, worse, a molecule within a cell — and if we wanted to take a swim, we might just as well try swimming inside a large block of concrete. But this can’t really be the case, and only illustrates the difficulty of transporting ourselves in imagination to a different scale of existence. Objects like you and I — or pebbles and flowers, or the gears and levers of a machine — could not be scaled down to a sub-cellular level and still remain what they were in any meaningful sense. They would become objects of an entirely different character.

Further, molecules “live” at a radically reduced scale compared to the cell, so in moving from the whole cell to the molecular level (what I will call the “microworld”), we see the various lawful relations changing yet again. In reality, molecules move through their cellular environs (as we will see below) with remarkable speed. Moreover, despite the example above, even cells move quite well in their viscous environment. So still other factors must come into play.

The motion, which gained the name “Brownian”, was further characterized by later investigators. Their work confirmed three features of the movements: they were indeed random in the sense that all directions were “equally likely”; “further motion seemed totally unrelated to past motion”; and “the motion never stopped”. In addition, “small particle size and low viscosity of the surrounding fluid resulted in faster motion” (Encyclopedia Britannica editors 2024).

In the early twentieth century the French physicist, Jean Baptiste Perrin, recorded the positions of three particles in water at 30-second intervals, as viewed through the microscope. His representation is shown in Figure 15.2.

Figure 15.2. Tracings of the motions in water of three colloidal particles of radius 0.53 microns, as seen under the microscope. Successive positions every 30 seconds are joined by straight line segments. The grid lines are 3.2 microns apart. Note that the straight lines are artifacts of the fact that positions were recorded at 30-second intervals. More frequent measurements would have yielded smoother curves (but the overall movement, with its directional changes, might still be termed “jerky”).⁴

Here is one example of the use of chemical energy. A single muscle cell contains hundreds of subunits (“sarcomeres”) whose dimensions are less than 3 millionths of a meter. They contract by converting chemical energy into mechanical energy. The force delivered by one sarcomere, as Albrecht-Buehler remarks, is such that “it can lift 60 entire cells! In other words, the cells submersed in violently jerking molasses of their surrounding aqueous media have literally gigantic forces at their disposal”.

The answer is that you would have to separate the electrons by approximately 200,000 light years. This hardly seems believable but is, I am assured on good authority,⁷ the correct answer. Two hundred thousand light years amounts to more than 34 billion times 34 billion miles. This is too much to get one’s head around, so the take-home point is simply that the electrical force is inconceivably stronger than the gravitational force.

The remarkable thing is that, in most of our routine experience of the world around us, we would hardly suspect the ubiquitous presence of such monstrous forces relative to our experience of gravity. This has to do with the fact that, in the world we normally experience, the bearers of negative electrical forces, such as electrons, are more or less counterbalanced by bearers of positive electrical forces, such as protons.

The way in which charged particles naturally tend to distribute themselves gets very complex, but the upshot of it all is the following: while the electrical forces between cellular constituents are unthinkably more powerful than the gravitational forces, they don’t simply rip the cell to smithereens. Here, too, negative and positive charges tend to balance each other out, but the operative word is “tend”. The imbalances that do exist are enough to help account for a lot of what goes on.

Albrecht-Buehler puts the matter this way: in the molecular collectives of cells, “[charged] molecules do not notice each other until they come closer than about one-third of their diameter. Once they are that close, however, they are attracted or repelled with almost irresistible electrical forces”. And again: a single electron charge within the typical electric field spanning a nerve membrane “can balance the weight of an entire cell”. He goes on to mention that “cell surfaces contain thousands of electron charges”.

We might also consider, not just static electrical forces, but electrical currents. Michael Persinger, the late Laurentian University (Canada) neuroscientist who investigated bioelectric phenomena in both the brain and the earth’s atmosphere, was looking, not for great differences, but for close parallels between the two widely varying scales. And he found them. But even here the parallels show how differently we must think, for example, of the brain compared to our routine picturing of physiological processes.

For example, the electrical impulse traveling along the axon of a neuron is driven by what might seem to be a trivial action potential of 0.09 volts. But this voltage applies across a 10 nanometer neuronal membrane, which means that it amounts to millions of volts per meter. This is on the order of the action potential of an atmospheric lightning bolt. And the density (amperes per square meter) of the current traveling along the neuronal path is, according to Persinger, “remarkably similar” to the density of the electric current flowing in a lightning bolt.

So the reality looks rather as if our brains are continually “lit up” by countless cascading, lightning-like discharges — perhaps on the order of a billion discharges per second (Persinger 2012).

This can happen because the chemical addition of another subunit to a polymer of the cytoskeleton is an energetic process. “The force of the addition of only one [protein] subunit is ten times larger than the weight of a cell!” In theory, therefore, “adding one subunit to a polymer could lift ten cells by the thickness of the subunit”. This tells us a good deal about how cells can move. At the normal scale of our lives we see nothing like this ability of a tiny unit of matter to be chemically joined to others of its kind and thereby to shift material objects (cells) that happen to be billions of times more massive than that tiny unit. (A typical human cell has been estimated to contain several billion protein molecules, in addition to water, lipids, carbohydrates, and all its other contents.)

Figure 15.3. Colorized scanning electron micrograph of a human T lymphocyte (also called a T cell) from the immune system of a healthy donor).⁸

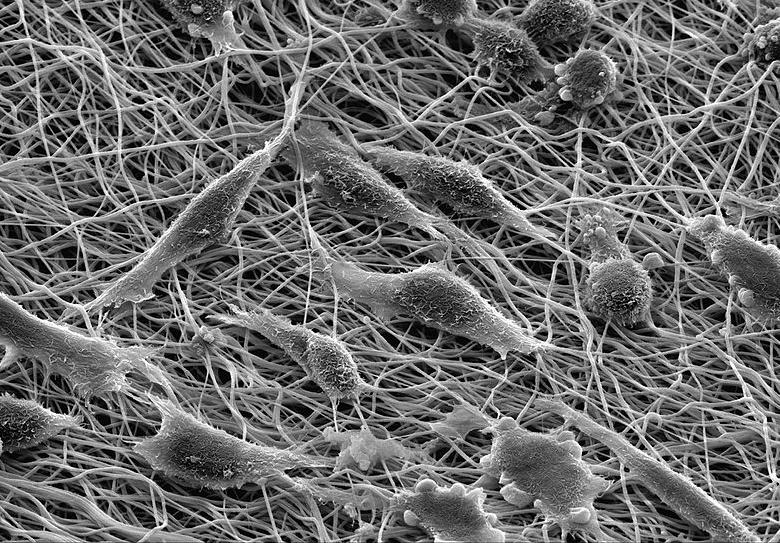
Figure 15.4. Scanning electron microscopy image of mouse fibroblasts cultured on artificial filamentous material.⁹

You will recall from our earlier discussion that a dew drop on a leaf is “pulled” into a sphere by its shaping forces. (See Figure 15.1.) Further, we heard that these forces, relative to the gravitational force that might break the droplet’s form and cause it to flow over the flat surface of the leaf, become vastly greater at very small scales. At the level of a cell, one of these shaping forces (surface tension) is “several thousand times larger than the weight of the cell, and we should expect the surface force to shape the cell as a perfect sphere”.

The question, therefore, is why a cell is not held rigidly in the shape of a sphere (Figures 15.3 and 15.4). Cells often have all sorts of non-spherical protrusions, and some kinds of cell readily flatten themselves against a surface and slide over it. In doing so, they are overcoming the hugely powerful shaping forces just mentioned. Part of the answer to this particular puzzle is, in Albrecht-Buehler’s words, that “the surface forces are no match for the strong polymerization forces”. Bundles of cytoskeletal filaments extending in a common direction have no difficulty re-shaping a cell and helping to bring it into movement.

Those “insanely high speeds” in crowded places are thought to explain how, as a standard textbook puts it, “a typical enzyme will catalyze the reaction of about a thousand substrate molecules every second” — meaning that the enzyme must bind to a new substrate in a fraction of a millisecond. This happens despite the fact that there tend to be relatively few substrate molecules per cell. If, for example, there is only 1 substrate molecule for every 100,000 water molecules, “nevertheless, the active site [the place where catalysis occurs] on an enzyme molecule that binds this substrate will be bombarded by about 500,000 random collisions with the substrate molecule per second”. At the same time, “a large globular protein [like many enzymes] is constantly tumbling, rotating about its axis about a million times per second” (Alberts et al. 2002, pp. 77-78).

As if everything we have heard so far is not difficult enough to comprehend, the problem of imagining microworlds truthfully is greatly magnified by emerging technologies that generate seductive images. When biologists speak so casually of atoms and molecules as things, and when engineers then present us with “pictures” of them, we can hardly help taking the pictures as images of actual phenomena. And so they are. But the phenomena we are dealing with are not “down there”. They are “up here”, where we are experiencing our instruments. Those instruments may be telling us something truthful about the microworld, but we have to figure out what that something is.

Figure 15.5. An image produced by the interaction of a non-contact atomic force microscope with graphene (a lattice of carbon atoms), in an IBM laboratory. The bright green lines forming approximate hexagons are taken to represent the molecular bonds between carbon atoms.¹¹

Figure 15.5, which is said to represent carbon atoms, is not in any normal sense a photograph of atoms, as the scientists and engineers who produce such images well know. There is no “thing” anywhere in the world that looks like this, except the picture itself. Responsible physicists do not talk about things at this level of observation at all. In this particular case we are looking at a kind of colored graph of a data set produced by an atomic force microscope. The spatial distribution of the artificial colors represents the relations between the highly refined measuring instrument, on one hand, and forces at an extremely small (atomic) scale, on the other. It is a picture of a distribution of forces. Forces are not things.

The one thing we can be sure of is that the cellular realm is not composed of anything like our familiar objects, only made smaller. The really foundational question is whether, and at what scale of observation, we are justified in talking about “things” at all, as opposed to forces or potentials.¹² This question certainly bears on the common appeal by molecular biologists to machine and computer models. Regarding computers, Albrecht-Buehler has written:

To my knowledge, there is not even a clue as to how to build a liquid miniature computer that would function despite thermal fluctuations and other turbulences in the liquid that would disrupt the circuitry (Albrecht-Buehler 1985).

There is, quite simply, nothing there that could remotely qualify as “circuitry” in the sense of “machine parts”.

One might have thought that the puzzling revelations from our indirect, instrument-mediated encounters with the microworld would have opened up a space for free inquiry as we considered the nature of perceptible, material appearance versus the theoretical constructs and misleading imagery through which we try to picture a realm of which we have no direct experience. One might indeed have expected that — given a microworld considered fundamental to our understanding yet inaccessible to the direct activity of our senses — we might have warned ourselves about the temptation to project falsely imagined perceptual contents into what is an experiential blank for us.

And, given the scientific commitment to empirical (experience-based) evidence, what are we to make of a microworld characterized almost solely in terms of thought-models, mathematical formulae, and theoretical constructs, with no sense experience to ground us? All we have really asked of our models and theoretical constructs — from the solid, indivisible atom of Dalton to the “solar-system” atom of Bohr to the probability clouds of our own day is that they be successful technologically, enabling us to make things (including scientific instruments) that work. And each model has in fact helped us to make things — until it didn’t. This practical goal has always been the essence of trial-and-error methods, and our models have become little more than helpful tools for wonderfully expediting such methods.

But, so far anyway, it is still hard to repress the occasional question: “How much do we actually understand?”

Notes

1. As the size of an animal decreases, its volume (and therefore its weight) decreases much more rapidly than its surface area. In other words, as any given object is reduced in size, its surface-to-volume (surface-to-weight) ratio rises. The increased surface-to-weight ratio of the mouse is why its rate of fall is reduced by air resistance more than the elephant’s rate of fall. A falling leaf is a more extreme example.

More significantly for the fate of the mouse and the elephant in our rather twisted thought experiment, the different surface-to-weight ratios mean that the weight of the mouse per square centimeter of its body surface striking the ground is minuscule compared to the weight overlying the elephant’s area of contact with the ground. So the crushing effect of the impact is much greater for the larger animal.

2. Among the interrelated shaping forces of a liquid such as water are internal cohesion and surface tension.

3. Figure 15.1 credit: Michael Apel (CC BY-SA 3.0).

4. Figure 15.2 credit: Original observations made by Jean Baptiste Perrin. Digital rendering by MiraiWarren (Public Domain, via Wikimedia Commons).

5. The word “collisions” suggests an activity of particles conceived in the manner of our everyday experience of tiny bits of matter. Thinking of water molecules in this way is not something any physicist today would want to defend.

6. It is worth remembering that the lives of large, multicellular organisms — ourselves, for example — are not centered upon the cellular and molecular level. As we walk, run, and otherwise pursue our lives on earth, our bodies must work against the pull of gravity. If we do not sufficiently perform that work — if we are bedridden or live a sedentary life-style — our bodies suffer ill effects.

We know further that the weightlessness endured by astronauts on long missions results in significant loss of bone mass, density, and strength (Keyak 2009). Likewise, lions raised in zoos, apart from the rigors and stresses of hunting and the need to patrol large territories, have a bone structure differing from lions raised in the wild (Holdrege 1998).

So Albrecht-Buehler’s assertion that “gravity is an entirely irrelevant force in the violently chaotic world of cells”, while it may be true when we are looking at the interplay of forces in the decontextualized cell, can hardly be true for cells in the context of our bodies. If someone experiences changes in bone mass and muscle strength while living in a gravity-free environment, this implies radical changes in cells, including the loss (death) of cells. The fact that, when a person stands upright on earth, the weight of a 150-pound body comes to bear upon the small surface area of two feet certainly makes gravity a “relevant force” for the tissues and cells on the bottoms of our feet. And much the same can be said about the distribution of weight and weight-bearing surfaces throughout our bodies.

Actually, the importance of a larger context was very much part of Albrecht-Buehler’s argument in his paper. He was claiming, quite rightly, that we cannot explain either cellular or organismic behavior by trying to ground our picture upon decontextualized molecular-level analyses.

7. I have this answer courtesy of the physicist, George Burnett-Stuart.

8. Figure 15.3 credit: NIAID/NIH (CC BY 2.0).

9. Figure 15.4 credit: Judyta Dulnik (CC BY-SA 4.0).

10. Callier 2021, citing a comparison offered by Anthony Hyman, a British cell biologist and a director of the Max Planck Institute of Molecular Cell Biology and Genetics in Dresden.

11. Figure 15.5 credit: IBM Research–Zurich (CC BY 2.0).

12. Some experimental techniques do give us a form of sense-perceptible report from the microworld. For example, the relatively small “green fluorescent protein” (GFP) can be fused to particular molecules of interest in a cell. When the cell is irradiated with blue or ultraviolet light, the protein fluoresces, revealing under a light microscope the distribution of the target molecules in a cellular location. Again, however, blobs of fluorescent light, while informative of location, do not give us pictures of molecular “objects” residing at that location.

When a student collects a quantity of DNA on a glass rod, she is not looking at DNA molecules, but rather at a white, sticky substance. Similarly, a prospector may be looking at a chunk of iron ore, but he is not examining iron atoms. To say that our instruments, by eliciting responses at an atomic scale, can trace significant structure at that scale, is not to answer in any meaningful experiential sense, “structure of what?” — not if by “what” we refer to objects of the microworld possessing sense-perceptible, material descriptions. We can legitimately relate the structure to white, sticky substance or to iron ore, but not to atomic particles imagined in the mode of that substance or that ore.

As a hypothetical question: what would we “see” if, through some sort of inner work, we should develop in the future a cognitive (clairvoyant?) capacity to experience — bring to appearance — whatever can be found, say, at the quantum level? This is, of course, pure speculation. But my surmise is that we would discover an intricately structured play of “forces” of will. We would discover, that is, a field of potential that, when probed in appropriate ways, can be brought to manifestation as materially engaged force. The fact that our own wills (in a manner of which we are completely ignorant and unaware) can take form in the enfleshed mechanical forces of our arms and legs might be suggestive in this regard.

This document: https://bwo.life/bk/microworld.htm

Steve Talbott :: Puzzles of the Microworld